All this is of course intended for the purpose of establishing the climate sensitivity of CO2.

So let’s assume that we managed to get an accurate representation of the number of layers, by using physics or empirical data, and that the number of layers is determined by the number of greenhouse gas molecules. Then it is easy to double the number of layers that are attributed to CO2, and see what happens with the radiation, and hence with the energy balance of the earth.

In the third chapter we calculated that the number of layers is app. 100.
Numbers about the share of CO2 in the greenhouse effect I found on internet varied widely and had a huge inaccuracy, but averaged on 14%.
Assuming that CO2 contributes app. 14% to the greenhouse effect, it provides app 14 layers of the 100. So a doubling of CO2 would increase the number of layers to 114.

First the 100 layer simulation with Surface Upward radiation (Su), and rather randomly Latent Heat (LH), convection and solar IR (SIR) included (double click to enlarge):

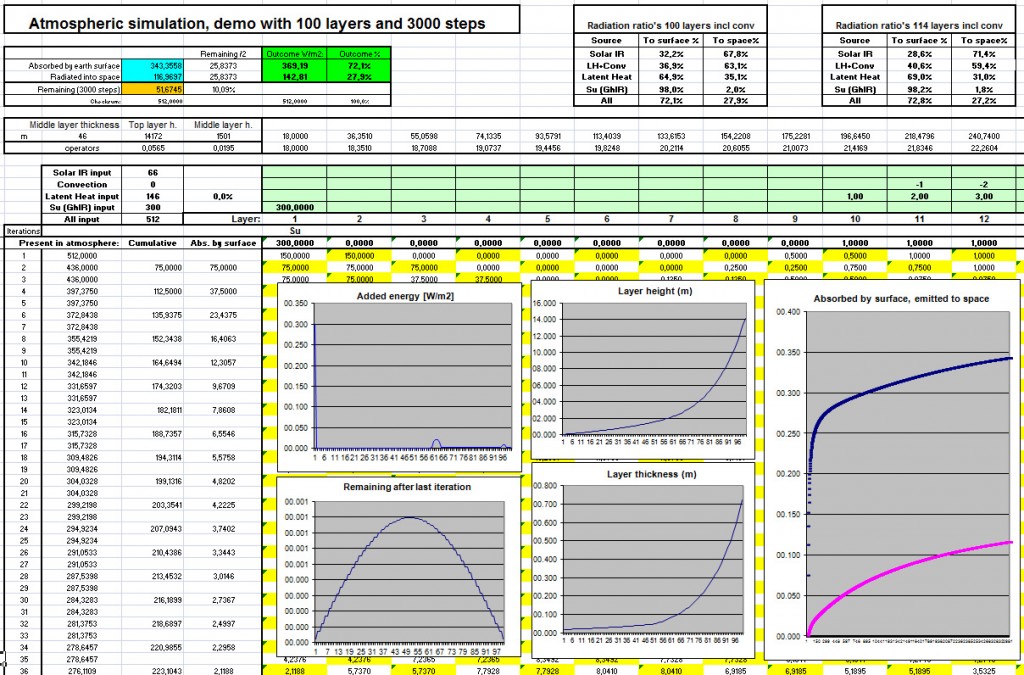
100 layers 3000 it
It turns out that with 100 layers, the downwards radiation Ed is 369,19 W/m2  (72.1%) vs a radiation to space of 142.81 W/m2  (27.9%)

Enjoy playing with the 100 layers simulation here!

Then the 114 layers simulation, where I left the Latent Heat in the same layers but inserted the Solar Incoming Radiation 14 layers higher, and “stretched” convection with 7 layers:

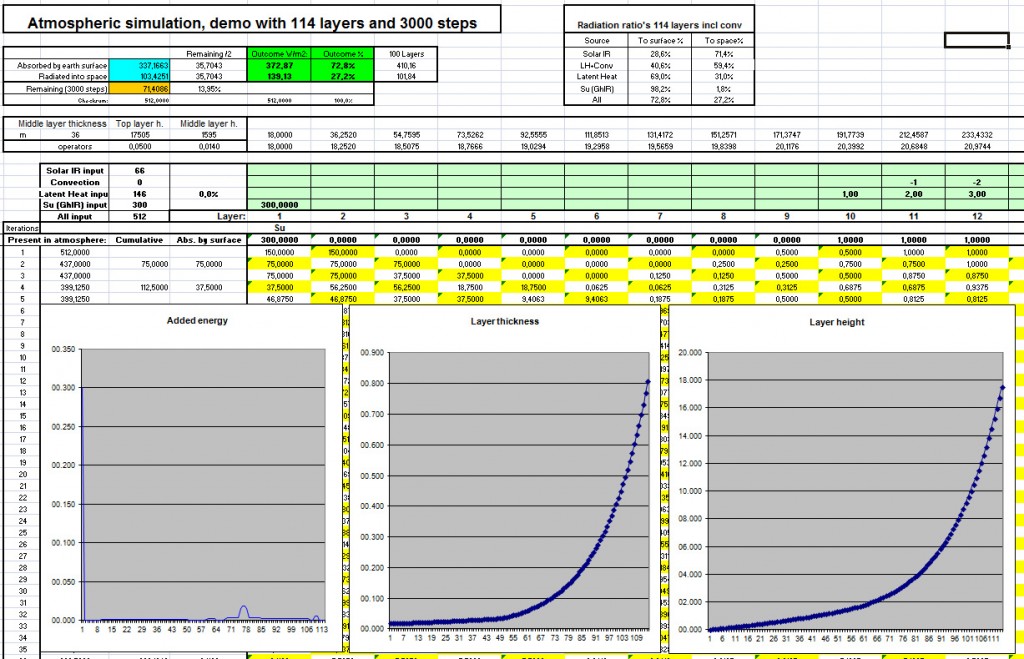
114 layers 3000 it
It turns out that with 114 layers, the Ed is 372.87 W/m2 (72.8%) vs a radiation to space of 139.13W/m2 (27.2%)

The difference is 3.75 W/m2, which is remarkably close to the 3,7 W/m2, that is generally accepted as the primary CO2 climate sensitivity.
I consider this to be a coïncidence, because as far as I know, standard calculations of the greenhouse effect only look at back radiation, while my calculation includes solar and latent heat energy, which in the next chapter will appear to be much stronger forcings than back radiation.

Enjoy playing with the 114 layers simulation here!

Caution!
It should be noted here that the layers where I inserted the LHT, the convection and the solar IR are, so far, my best guess, so the outcome is dubious at least. An experts estimation would no doubt improve this part of the model considerably.

For now the model is most of all a demonstration of how the Fireworks theory could be used to get quite exact results, that contain no hidden tricks or fiddlings that only the model maker knows. This is all straightforward, and clear for everybody to control, or to play with, by entering the data and premisses that he considers right.

The re-radiation question
When just entering the GhIR that is radiated from the surface as energy input, and leaving out downward radiation from latent heat and solar IR, the fireworks simulation gives quite exact results, because the ratio Eu/Ed is only determined by the number of layers.

So this is what comes out:

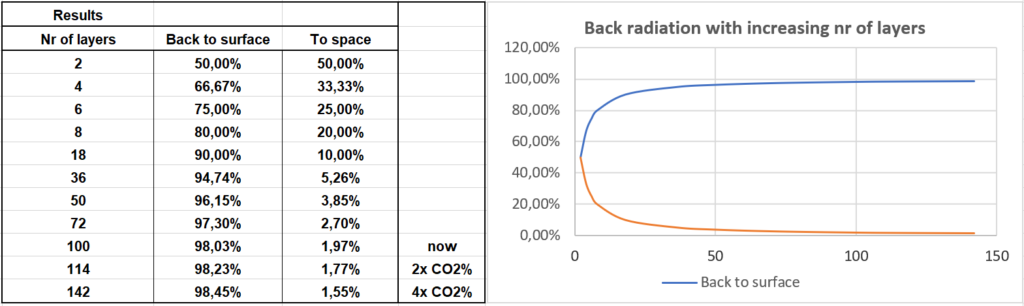
It is not easy to compare this outcome with pyrgiometer data, because those also contain the back radiation by clouds, part of the absorbed  solar IR that reaches the surface, and most of all: the part of the latent heat that is absorbed by the atmosphere when condensating and is radiated downwards.

As the GhIR upwards from the surface is 297 W/m2, the difference for a doubling of CO2 resulting in an increase of 14 layers is 0,2% of 297 W/m2 = 0,59 W/m2 only.
For the next doubling with 28 layers to 142 layers in total, the increase in back radiation would be 0,65 W/m2.
Obviously, with current greenhouse gas concentrations, a CO2 doubling has a marginal influence on surface warming, as far as back radiation is concerned.

Next step
This simulation does not answer the main question: will climate react to a CO2 increase with a positive or negative feed back. I am still working on that topic, as you can read in my first findings, as are proposed for discussion in chapter 6 to 11.