In order to explain the physics of the greenhouse effect, it is often proposed that it works in the following way:
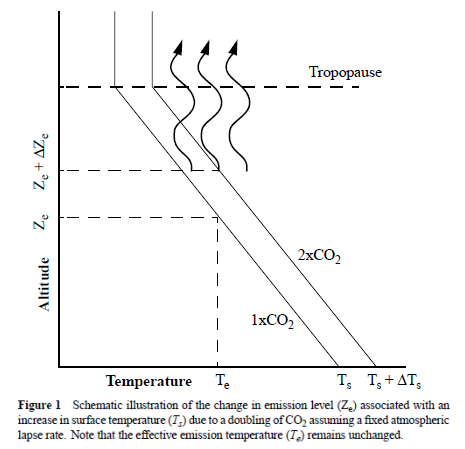
Because, with an increase in CO2 concentration in the atmosphere, there are more CO2 greenhouse molecules in the tropopause, they will radiate into space from a higher level (from Ze to Ze + ΔZe). Because of the adiabatic lapse rate, it will be colder there, so they will radiate (a lot!) less energy to space.
This disturbs the equilibrium, so in order to restore that, the earth surface has to heat up (from Ts to Ts + ΔTs), so the adiabatic lapse rate (ALR) will move upwards and warm the tropopause, until the radiation into space is the same as before the CO2 increase. In the drawings this theory is always illustrated with beautifully straight lines.
This explanation seems quite logical, and many adhere to it. But I think I can prove that the logic behind it is flawed.
Wrong assumption
The flaw of the theory is that it contains a hidden assumption that is not correct.
It assumes that the energy that is absorbed at the surface, is transported to the tropopause by the rising air folowing the lapse rate, and is emitted to space from there.
The first assumption is correct, which indeed results in the temperature in the rising air folowing an adiabatic lapse rate (ALR), somewhere between the dry (DALR) and the saturated (SALR) adiabatic lapse rate, for obvious reasons on or very close to the SALR.
The second assumption however is not correct: the energy that the rising air contains is not emitted to space from the top of the ALR line at the crossing of the Ts en Ze lines. It cannot be emitted there, because the temperature at that height is extremely low (-50C to -100C), and the emission of the GHG decreases with T^4. Apart from that, the GHG concentration is extremely low there, because there is hardly any water vapour left due to the low temperature, and also the CO2 concentration is low because of the lower pressure.
Trapped air
In reality the air hardly cools down after reaching the tropopause, cannot rise any higher because the air above it is warmer, and it cannot descend, because the air below it is colder. So it starts to float away to places with less convection. This floating continues untill the very low emission of the GHG has managed to lower the temperatur enough so that it can decend following the DALR line, while remaing cooler than the air around it. This temperature decrease has to compensate the difference between the SALR that was leading in the rising part of the cycle, and the DALR that it has to follow while descending. This can take a very long time. And still most of the energy that it transported to the tropopause remains contained in this air, as we will calculate in the next chapter. This remaining energy is emitted to space while heating up fast during the descent, helped by the fact that there are very few GHG molecules above it to prevent the emission to space, because the descending air is extremely dry. This cycle will be quantified in the next chapter.
For now it suffices to say that the energy is not emitted from emission level Ze at the upper end of the ALR line from the surface. If it is not, than an increase in GHG will not push the ALR to a higher emission level Ze + ΔZe, resulting in an increased surface temperature Ts + ΔTs. As I will calculate in the next chapter, an increased GHG concentration can very well be compensated by an increase in convection, without an increase of the surface temperature.
Calculated surface and atmosphere warming
My fireworks simulation calculates exactly what happens with the energy in the tropopause as well as at the surface, and tells us how much is absorbed and emitted. The surface heating effect of a CO2 increase is clear, and so is the decrease in energy that is radiated to space, but the first is not influenced by the second, and certainly not by the dry adiabatic lapse rate. The change in temperature of the surface is just the result of the increase in the number of layers, defined by the average free path for GhIR.
I am trying to establish the radiative effect on air temperature (and the ALR’s) at different heights. It seems possible to calculate that from the simulation data, but that is still a work in progress.
Concluding, the fireworks approach of radiation seems much more reliable than the simplified “logic” of the parallel moving adiabatic lapse rate in the standard greenhouse theory.
This chapter considered the radiation aspects of the standard greenhouse theory.
In chapter 10 I will look closer at the convection aspect of it, by analysing and calculating the Hadley Cell, using my simulation program.
This chapter has been considerably revised.