So far we only spoke about the radiation mechanisms.
Of course we need to include clouds, albedo and so on.
In fact, that was what I actually started with, and that is how I found out that I needed a radiation simulation.
I put every significant climate aspect I knew in a spreadsheet, and made an energy balance of it in the way Kiehl/Trenberth did.
I did this by dividing the radiative spectrum in sections with a specific behaviour, and calculated the energy flow for each of them. Combined they seemed to give quite good results.
Once again the basis is very simple and easy to understand, and everybody can vary all parameters to create his own preferred atmosphere.
In this scheme you can see the output of the 25 layer model I experimented a lot with:
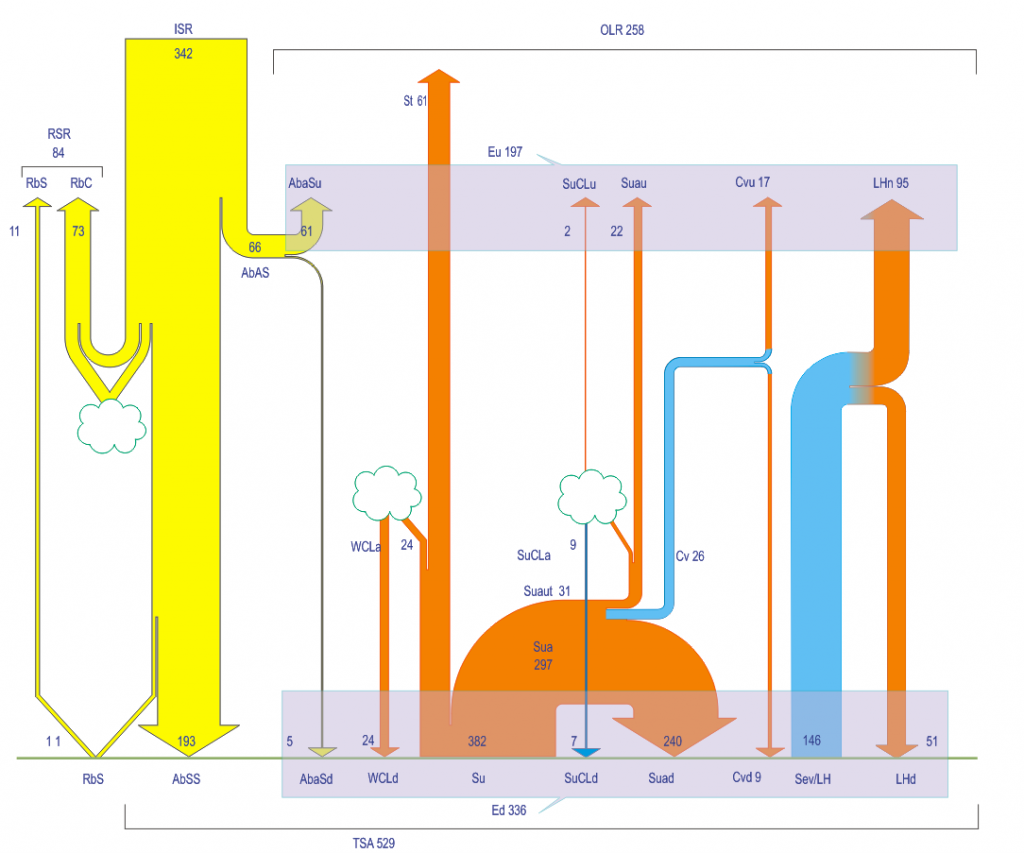
The hardest parameters to estimate were the radiative mechanisms that divide the absorbed IR energy in OLR and Ed.
This happens at four places:
– Surface upward absorbed: Sua
– Surface evaporation/Latent Heat: Sev/LH
– Convection: Cv
– Solar IR absorbed by atmosphere: AbAS
That is what forced me to build my simulation.
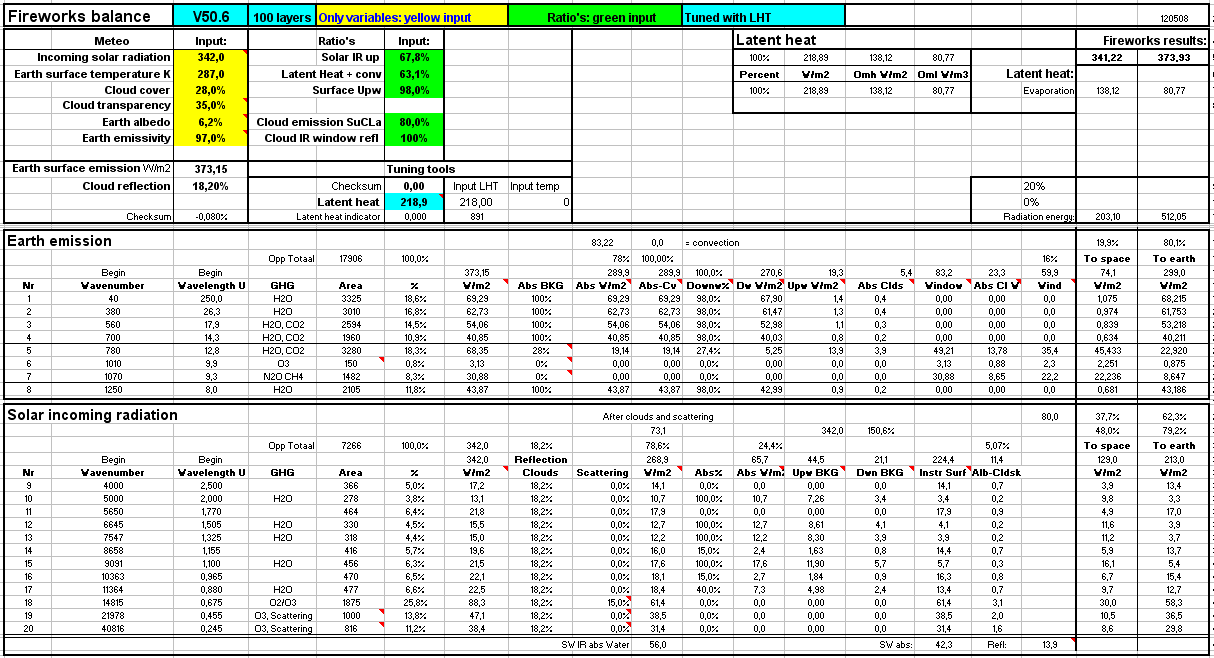
For a more accurate balance I needed to implement the 100/114 layer data.
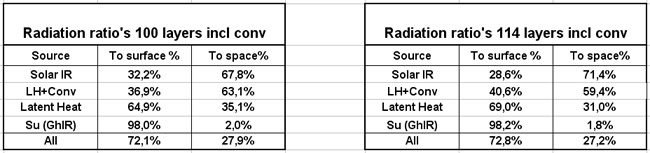
From the simulations with the still rather randomly distributed LHT and SolarIR, I got the following ratio’s of Ed/Eu in percents:
In the balance sheet these ratio’s determine the radiative mechanisms, and can be combined with the other parameters like reflection, albedo and clouds.
In the calculation I used the combined latent heat transport and convection ratio.
The sheet looks like this (click to enlarge):
I based the wavelength sections on bad graphs that I got from internet. I am sure that the right data are available to experts, but this is the best I could do.
Therefore, the outcome is not significant for now, but can easily be optimised by using the right data.
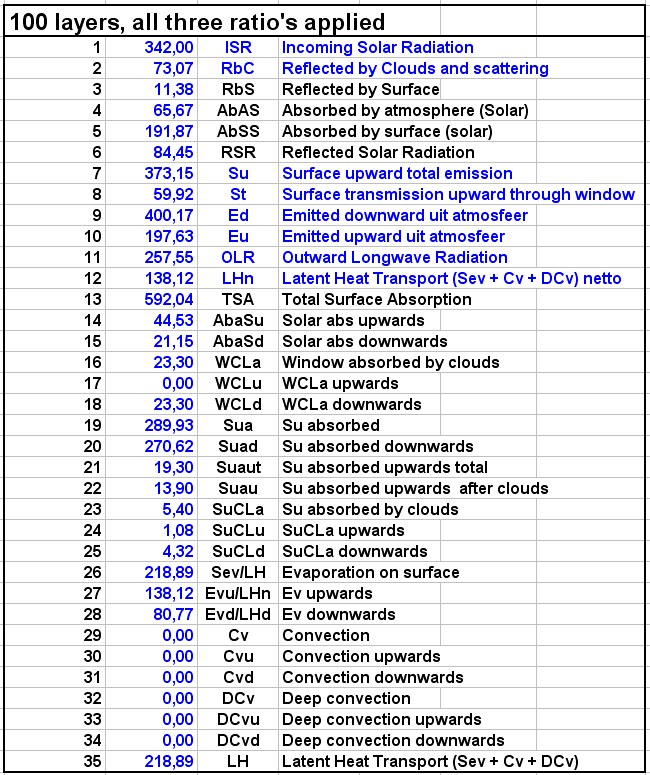
If I apply the ratio’s of the 100 layer simulation, I get this output:
(see the above scheme for the abbreviations):
Climate sensitivity
Now we have built a complete model of the atmosphere, so it is interesting to see what the climate sensitivity of a CO2 doubling is! In order to find that out, I have to apply the ratio’s I found in the simulations.
If I only apply the 114 layer ratio for the surface upward (Su) radiation, and I keep the influence of CO2 on latent heat and solar IR constant, I need to heat up the surface with 0,4 K to restore the equilibrium.
If I add the 114 layer solar incoming IR ratio, I have to lower the temperature of the surface with 1,8K.
But the increased CO2 also influences the radiation from energy that is brought in the atmosphere by condensation.
If I add the LH + convection radiation ratio for 114 layers, with the present attribution of layers to latent heat release, I need almost 6 K to restore the equilibrium, or an increased latent heat transport of 5%.
This outcome suggests that the CO2 concentration influence is far greater on the latent heat energy flow than on the LWIR that is emitted by the surface.
Conclusion
I need to stress once more that the outcome of any of these calculations is still quite dubious, because so many arbitrary assumptions have been made. But all these inaccuracies can be corrected by experts, most of them very easily. Once the input data are good, there is all reason to believe that the outcome will be useful and maybe even accurate too.
The great advantage would be that every person who can work with Excel, is able to see what the output is based on, understand each step from data input to the output, and play with it to get a grasp on the way climate works.
For now, I just hope that I managed to convince you that the set-up of the simulation and the balance model, based on the Fireworks theory, can really work, and that it is worth while trying to improve it.
Leave A Comment