2. The Fireworks atmospheric simulation
Once absorbed by a GHG molecule, the GhIR energy will be re-radiated and absorbed very many times before it will be radiated out into space or be absorbed by the surface.
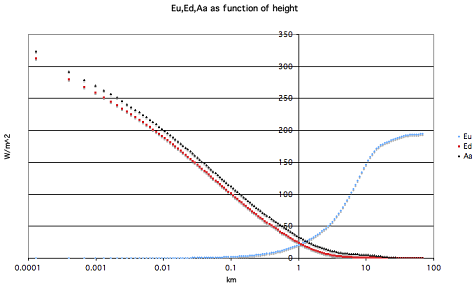
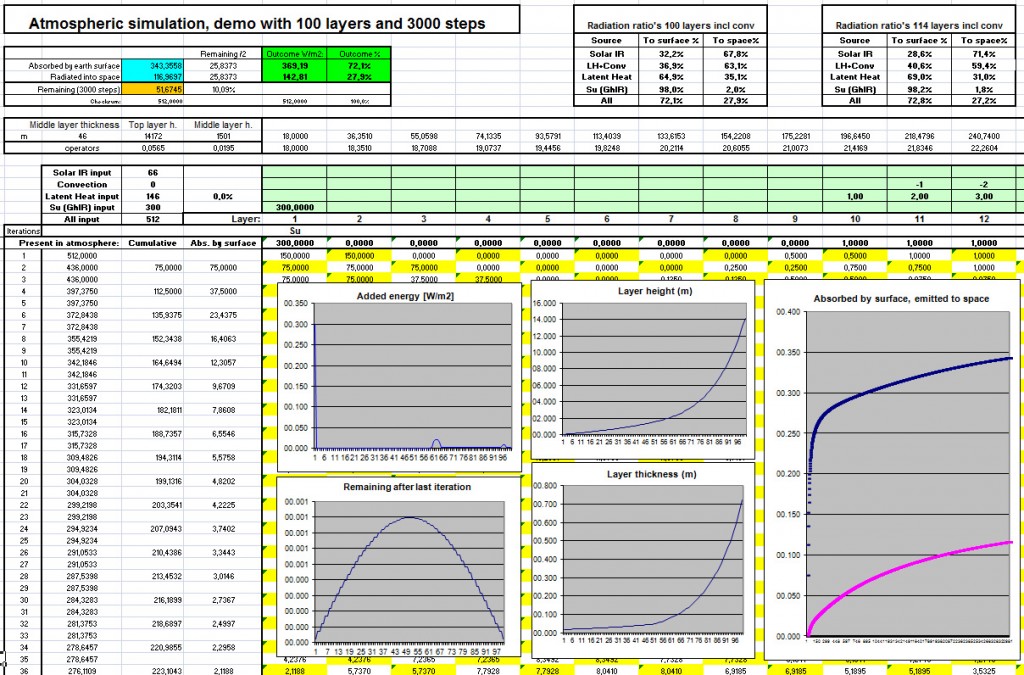
Describing this process quantitatively in formulas seemed to be impossible, at least for my mathematics skills. And as far as I know, even very skilled mathematicians have never been able to describe more than 7 layers in a mathematical model of the atmosphere. So I invented another way to calculate a large number of layers accurately, using an iteration approach.
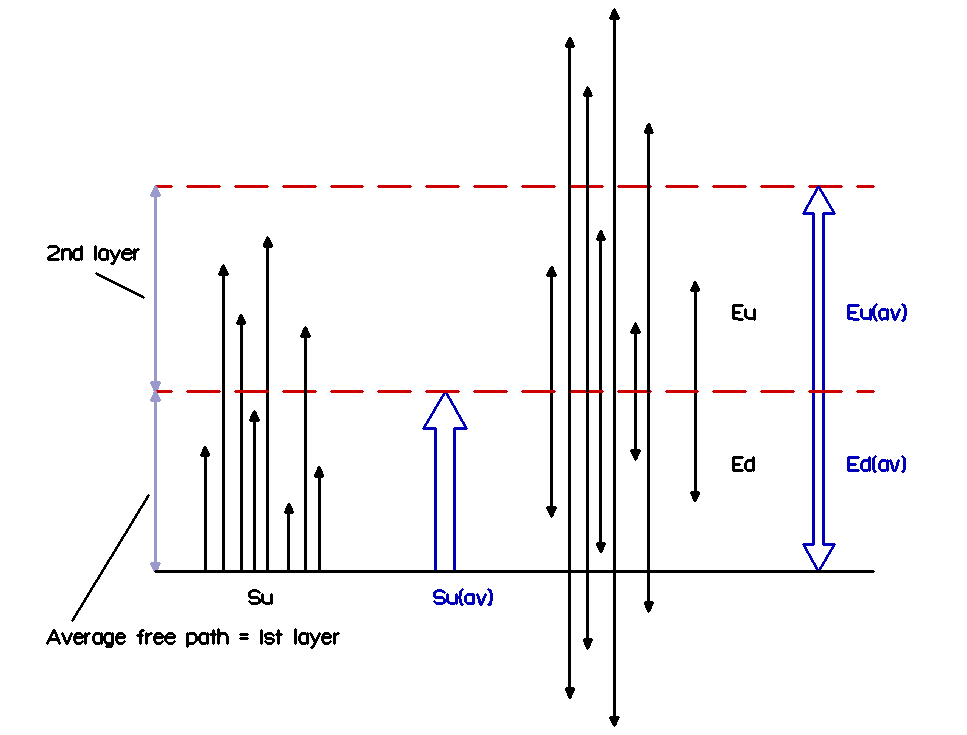
Let me first show the layer definition image of the first chapter:
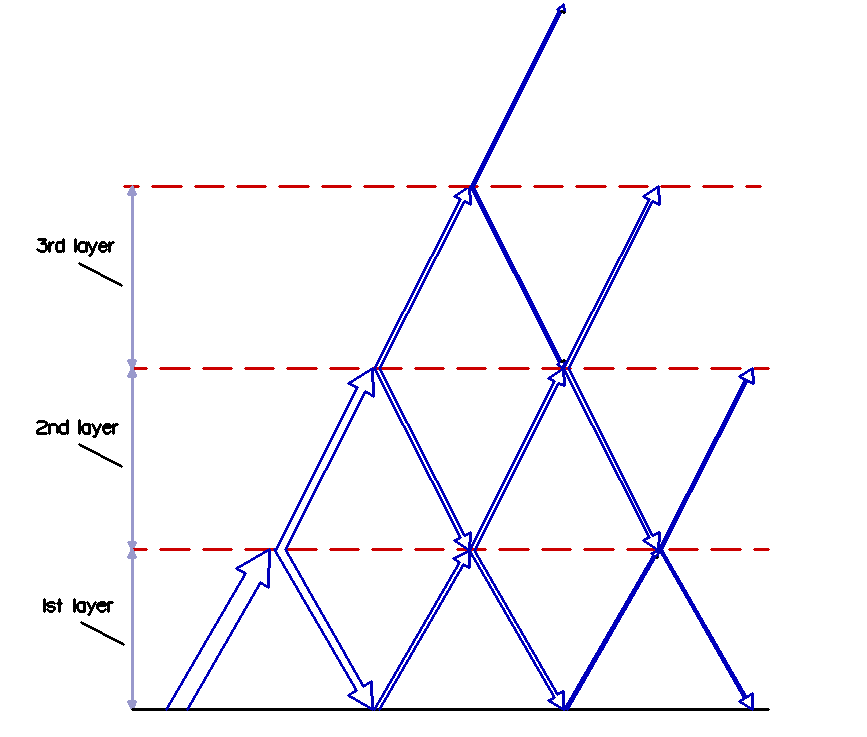
If I tilt the blue arrows a bit, a new image appears, that can clarify the formulas that I based my simulation on:
You see that Su is divided equally in Ed1 and Eu1.
Ed1 looses 50% to the surface, and Eu1 looses 50% to layer 3, so half of Ed1 and Eu1 (twice 25% of Su) will be re-radiated back to the top of layer 1. (more…)